Создать симуляцию Монте-Карло с помощью Excel. Моделирование методом Монте-Карло в Crystal Ball для Excel
Любая инвестиция нуждается в тщательных расчетах. Иначе инвестор рискует потерять вложенные средства.
На первый взгляд, бизнес прибыльный и привлекательный для инвестирования. Но это только первое впечатление. Необходим скрупулезный анализ инвестиционного проекта. И сделать это можно самостоятельно с помощью Excel, без привлечения дорогостоящих специалистов и экспертов по управлению инвестиционными портфелями.
Расчет инвестиционного проекта в Excel
Инвестор вкладывает деньги в готовое предприятие. Тогда ему необходимо оценить эффективность работы (доходность, надежность). Либо в новое дело – все расчеты проводятся на основе данных, полученных в ходе изучения рынка (инфраструктуры, доходов населения, уровня инфляции и т.д.).
Рассмотрим создание бизнеса с нуля. Рассчитаем прибыльность предприятия с помощью формул Excel. Для примера будем брать условные товары и цифры. Важно понять принцип, а подставить можно любые данные.
Итак, у нас есть идея открыть небольшой магазин. Определимся с затратами. Они бывают
- постоянными (нельзя рассчитать на единицу товара);
- переменными (можно рассчитать на единицу товара).
Первоначальные вложения – 300 000 рублей. Деньги расходуются на оформление предпринимательства, оборудование помещения, закупку первой партии товара и т.д.
Составляем таблицу с постоянными затратами:
* Статьи расходов индивидуальны. Но принцип составления - понятен.
По такому же принципу составляем отдельно таблицу с переменными затратами:

Для нахождения цены продажи использовали формулу: =B4*(1+C4/100).
Следующий этап – прогнозируем объем продаж, выручку и прибыль. Это самый ответственный этап при составлении инвестиционного проекта.

Объем продаж условный. В реальной жизни эти цифры – результат анализа доходов населения, востребованности товаров, уровня инфляции, сезона, места нахождения торговой точки и т.д.
Для подсчета выручки использовалась формула: =СУММПРОИЗВ(B3:B6;Лист2!$D$4:$D$7). Где первый массив – объемы продаж; второй массив – цены реализации.
Выручка минус переменные затраты: =B7-СУММПРОИЗВ(B3:B6;Лист2!$B$4:$B$7).
Прибыль до уплаты налогов: =B8-Лист1!$B$14 (выручка без переменных и постоянных затрат).
Налоги ЕНВД: =Лист1!A10*1800*0,15*3 (1800 – базовая доходность по виду деятельности, 3 – количество месяцев, С12 – площадь помещения).
Чистая прибыль: прибыль – налоги.
Оценка инвестиционного проекта в Excel
Рассчитывают 4 основных показателя:
- чистый приведенный эффект (ЧПЭ, NPV);
- индекс рентабельности инвестиций (ИРИ, PI);
- внутреннюю норму доходности (ВНД, IRR);
- дисконтированный срок окупаемости (ДСО, DPP).
Для примера возьмем следующий вариант инвестиций:

Сначала дисконтируем каждый положительный элемент денежного потока.
Создадим новый столбец. Введем формулу вида: = положительный элемент денежного потока / (1 + ставка дисконтирования)^ степень, равная периоду.
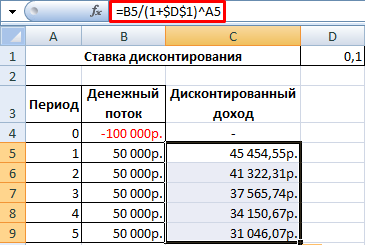
Теперь рассчитаем чистый приведенный эффект:

Найдем индекс рентабельности инвестиций. Для этого нужно разделить чистую приведенную стоимость (ЧПС) на объем инвестированных средств (со знаком «+»):

Результат – 1,90.
Посчитаем IRR инвестиционного проекта в Excel. Напомним формулу:
ВНД = ΣДП t / (1 + ВНР) t = И.
ДП t – положительные элементы денежного потока, которые нужно продисконтировать по такой ставке, чтобы чистый приведенный эффект равнялся нулю. Внутренняя норма доходности – такая ставка дисконтирования, при которой выпадает равенство вида:
ΣДП t / (1 + ВНР) t – И = 0,
Воспользуемся инструментом «Анализ «Что-Если»»:


Ставка дисконтирования равняется 0,41. Следовательно, внутренняя норма доходности составила 41%.
Моделирование рисков инвестиционных проектов в Excel
Используем метод имитационного моделирования Монте-Карло. Задача – воспроизвести развитие бизнеса на основе результатов анализа известных элементов и взаимосвязей между ними.
Продемонстрируем моделирование рисков на простейшем примере. Составим условный шаблон с данными:
Ячейки, которые содержат формулы ниже подписаны своими значениями соответственно.
Прогнозируемые показатели – цена услуги и количество пользователей. Под этими данными делаем запись «Результаты имитации». На вкладке «Данные» нажимаем «Анализ данных» (если там нет инструмента придется подключить настройку). В открывшемся окне выбираем «Генерация случайных чисел».

Заполняем параметры следующим образом:

Нам нужно смоделировать ситуацию на основе распределений разного типа.
Для генерации количества пользователей воспользуемся функцией СЛУЧМЕЖДУ. Нижняя граница (при самом плохом варианте событий) – 1 пользователь. Верхняя граница (при самом хорошем варианте развития бизнеса) – 50 покупателей услуги.

Скопируем полученные значения и формулы на весь диапазон. Для переменных затрат тоже сделаем генерацию случайных чисел. Получим эмпирическое распределение показателей эффективности проекта.

Чтобы оценить риски, нужно сделать экономико-статистический анализ. Снова воспользуемся инструментом «Анализ данных». Выбираем «Описательная статистика».

Программа выдает результат (по столбцу «Коэффициент эффективности»):


Можно делать выводы и принимать окончательное решение.
Не так давно я прочитал замечательную книгу Дугласа Хаббарда . В кратком конспекте книги я обещал, что одному из разделов – Оценка риска: введение в моделирование методом Монте-Карло – я посвящу отдельную заметку. Да всё как-то не складывалось. И вот недавно я стал более внимательно изучать методы управления валютными рисками. В материалах, посвященных этой тематике, часто упоминается моделирование методом Монте-Карло. Так что обещанный материал перед вами.
Приведу простой пример моделирования методом Монте-Карло для тех, кто никогда не работал с ним ранее, но имеет определенное представление об использовании электронных таблиц Excel.
Предположим, что вы хотите арендовать новый станок. Стоимость годовой аренды станка 400 000 дол., и договор нужно подписать на несколько лет. Поэтому, даже не достигнув , вы всё равно не сможете сразу вернуть станок. Вы собираетесь подписать договор, думая, что современное оборудование позволит сэкономить на трудозатратах и стоимости сырья и материалов, а также считаете, что материально-техническое обслуживание нового станка обойдется дешевле.
Скачать заметку в формате , примеры в формате
Ваши калиброванные специалисты по оценке дали следующие интервалы значений ожидаемой экономии и годового объема производства:
Годовая экономия составит: (MS + LS + RMS) х PL
Конечно, этот пример слишком прост, чтобы быть реалистичным. Объем производства каждый год меняется, какие-то затраты снизятся, когда рабочие окончательно освоят новый станок, и т.д. Но мы в этом примере намеренно пожертвовали реализмом ради простоты.
Если мы возьмем медиану (среднее) каждого из интервалов значений, то получим годовую экономию: (15 + 3 + 6) х 25 000 = 600 000 (дол.)
Похоже, что мы не только добились безубыточности, но и получили кое-какую прибыль, но не забывайте – существуют неопределенности. Как же оценить рискованность этих инвестиций? Давайте, прежде всего, определим, что такое риск в данном контексте. Чтобы получить риск, мы должны наметить будущие результаты с присущими им неопределенностями, причем какие-то из них – с вероятностью понести ущерб, поддающийся количественному определению. Один из способов взглянуть на риск – представить вероятность того, что мы не добьемся безубыточности, то есть что наша экономия окажется меньше годовой стоимости аренды станка. Чем больше нам не хватит на покрытие расходов на аренду, тем больше мы потеряем. Сумма 600 000 дол. – это медиана интервала. Как определить реальный интервал значений и рассчитать по нему вероятность того, что мы не достигнем точки безубыточности?
Поскольку точные данные отсутствуют, нельзя выполнить простые расчеты для ответа на вопрос, сможем ли мы добиться требуемой экономии. Есть методы, позволяющие при определенных условиях найти интервал значений результирующего параметра по диапазонам значений исходных данных, но для большинства проблем из реальной жизни такие условия, как правило, не существуют. Как только мы начинаем суммировать и умножать разные типы распределений, задача обычно превращается в то, что математики называют неразрешимой или не имеющей решения обычными математическими методами проблемой. Поэтому взамен мы пользуемся методом прямого подбора возможных вариантов, ставшим возможным благодаря появлению компьютеров. Из имеющихся интервалов мы выбираем наугад множество (тысячи) точных значений исходных параметров и рассчитываем множество точных значений искомого показателя.
Моделирование методом Монте-Карло – превосходный способ решения подобных проблем. Мы должны лишь случайным образом выбрать в указанных интервалах значения, подставить их в формулу для расчета годовой экономии и рассчитать итог. Одни результаты превысят рассчитанную нами медиану 600 000 дол., а другие окажутся ниже. Некоторые будут даже ниже требуемых для безубыточности 400 000 дол.
Вы легко сможете осуществить моделирование методом Монте-Карло на персональном компьютере с помощью программы Excel, но для этого понадобится чуть больше информации, чем 90%-ный доверительный интервал. Необходимо знать форму кривой распределения. Для разных величин больше подходят кривые одной формы, чем другой. В случае 90%-ного доверительного интервала обычно используется кривая нормального (гауссова) распределения. Это хорошо знакомая всем колоколообразная кривая, на которой большинство возможных значений результатов группируются в центральной части графика и лишь немногие, менее вероятные, распределяются, сходя на нет к его краям (рис. 1).
Вот как выглядит нормальное распределение:
Рис.1. Нормальное распределение. По оси абсцисс число сигм.
Особенности:
- значения, располагающиеся в центральной части графика, более вероятны, чем значения по его краям;
- распределение симметрично; медиана находится точно посредине между верхней и нижней границами 90%-ного доверительного интервала (CI);
- «хвосты» графика бесконечны; значения за пределами 90%-ного доверительного интервала маловероятны, но все же возможны.
Для построения нормального распределения в Excel можно воспользоваться функцией =НОРМРАСП(Х; Среднее; Стандартное_откл; Интегральная), где
Х – значение, для которого строится нормальное распределение;
Среднее – среднее арифметическое распределения; в нашем случае = 0;
Стандартное_откл – стандартное отклонение распределения; в нашем случае = 1;
Интегральная – логическое значение, определяющее форму функции; если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения; в нашем случае = ЛОЖЬ.
Говоря о нормальном распределении, необходимо упомянуть о таком связанном с ним понятии, как стандартное отклонение. Очевидно, не все обладают интуитивным пониманием, что это такое, но поскольку стандартное отклонение можно заменить числом, рассчитанным по 90%-ному доверительному интервалу (смысл которого интуитивно понимают многие), я не буду здесь подробно на нем останавливаться. Рисунок 1 показывает, что в одном 90%-ном доверительном интервале насчитывается 3,29 стандартного отклонения, поэтому нам просто нужно будет сделать преобразование.
В нашем случае следует создать в электронной таблице генератор случайных чисел для каждого интервала значений. Начнем, например, с MS – экономии на материально-техническом обслуживании. Воспользуемся формулой Excel: =НОРМОБР(вероятность;среднее;стандартное_откл), где
Вероятность – вероятность, соответствующая нормальному распределению;
Среднее – среднее арифметическое распределения;
Стандартное_откл – стандартное отклонение распределения.
В нашем случае:
Среднее (медиана) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2;
Стандартное отклонение = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29.
Для параметра MS формула имеет вид: =НОРМОБР(СЛЧИС();15;(20-10)/3,29), где
СЛЧИС – функция, генерирующая случайные числа в диапазоне от 0 до 1;
15 – среднее арифметическое диапазона MS;
(20-10)/3,29 = 3,04 – стандартное отклонение; напомню, что смысл стандартного отклонения в следующем: в интервал 3,29*Стандарт_откл, расположенный симметрично относительного среднего, попадает 90% всех значений случайной величины (в нашем случае MS)
Распределение величины экономии на материально-техническом обслуживании для 100 случайных нормально распределенных значений:
Рис. 2. Вероятность распределения MS по диапазонам значений; о том, как построить такое распределение с помощью сводной таблицы см.
Поскольку мы использовали «лишь» 100 случайных значений, распределение получилось не таким уж и симметричным. Тем не менее, около 90% значений попали в диапазон экономии на MS от 10 до 20 долл. (если быть точным, то 91%).
Построим таблицу на основе доверительных интервалов параметров MS, LS, RMS и PL (рис. 3). Два последних столбца показывают результаты расчетов на основе данных других столбцов. В столбце «Общая экономия» показана годовая экономия, рассчитанная для каждой строки. Например, в случае реализации сценария 1 общая экономия составит (14,3 + 5,8 + 4,3) х 23 471 = 570 834 долл. Столбец «Достигается ли безубыточность?» вам на самом деле не нужен. Я включил его просто для информативности. Создадим в Excel 10 000 строк-сценариев.
Рис. 3. Расчет сценариев методом Монте-Карло в Excel
Чтобы оценить полученные результаты, можно использовать, например, сводную таблицу, которая позволяет подсчитать число сценариев в каждом 100-тысячном диапазоне. Затем вы строите график, отображающий результаты расчета (рис. 4). Этот график показывает, какая доля из 10 000 сценариев будут иметь годовую экономию в том или ином интервале значений. Например, около 3% сценариев дадут годовую экономию более 1М дол.
Рис. 4. Распределение общей экономии по диапазонам значений. По оси абсцисс отложены 100-тысячные диапазоны размера экономии, а по оси ординат доля сценариев, приходящихся на указанный диапазон
Из всех полученных значений годовой экономии примерно 15% будут меньше 400К дол. Это означает, что вероятность ущерба составляет 15%. Данное число и представляет содержательную оценку риска. Но риск не всегда сводится к возможности отрицательной доходности инвестиций. Оценивая размеры вещи, мы определяем ее высоту, массу, обхват и т.д. Точно так же существуют и несколько полезных показателей риска. Дальнейший анализ показывает: есть 4%-ная вероятность того, что завод вместо экономии будет терять ежегодно по 100К дол. Однако полное отсутствие доходов практически исключено. Вот что подразумевается под анализом риска – мы должны уметь рассчитывать вероятности ущерба разного масштаба. Если вы действительно измеряете риск, то должны делать именно это.
В некоторых ситуациях можно пойти более коротким путем. Если все распределения значений, с которыми мы работаем, будут нормальными и нам надо просто сложить интервалы этих значений (например, интервалы затрат и выгод) или вычесть их друг из друга, то можно обойтись и без моделирования методом Монте-Карло. Когда необходимо суммировать три вида экономии из нашего примера, следует провести простой расчет. Чтобы получить искомый интервал, используйте шесть шагов, перечисленных ниже:
1) вычтите среднее значение каждого интервала значений из его верхней границы; для экономии на материально-техническом обслуживании 20 – 15 = 5 (дол.), для экономии на трудозатратах – 5 дол. и для экономии на сырье и материалах – 3 дол.;
2) возведите в квадрат результаты первого шага 5 2 = 25 (дол.) и т.д.;
3) суммируйте результаты второго шага 25 + 25 + 9 = 59 (дол.);
4) извлеките квадратный корень из полученной суммы: получится 7,7 дол.;
5) сложите все средние значения: 15 + 3 + 6 = 24 (дол.);
6) прибавьте к сумме средних значений результат шага 4 и получите верхнюю границу диапазона: 24 + 7,7 = 31,7 дол.; вычтите из суммы средних значений результат шага 4 и получите нижнюю границу диапазона 24 – 7,7 = 16,3 дол.
Таким образом, 90%-ный доверительный интервал для суммы трех 90%-ных доверительных интервалов по каждому виду экономии составляет 16,3–31,7 дол.
Мы использовали следующее свойство: размах суммарного интервала равен квадратному корню из суммы квадратов размахов отдельных интервалов .
Иногда нечто похожее делают, суммируя все «оптимистические» значения верхней границы и «пессимистические» значения нижней границы интервала. В данном случае мы получили бы на основе наших трех 90%-ных доверительных интервалов суммарный интервал 11–37 дол. Этот интервал несколько шире, чем 16,3–31,7 дол. Когда такие расчеты выполняются при обосновании проекта с десятками переменных, расширение интервала становится чрезмерным, чтобы его игнорировать. Брать самые «оптимистические» значения для верхней границы и «пессимистические» для нижней – все равно что думать: бросив несколько игральных костей, мы во всех случаях получим только «1» или только «6». На самом же деле выпадет некое сочетание низких и высоких значений. Чрезмерное расширение интервала – распространенная ошибка, которая, несомненно, часто приводит к принятию необоснованных решений. В то же время описанный мной простой метод прекрасно работает, когда у нас есть несколько 90%-ных доверительных интервалов, которые необходимо суммировать.
Однако наша цель не только суммировать интервалы, но и умножить их на объем производства, значения которого также даны в виде диапазона. Простой метод суммирования годится только для вычитания или сложения интервалов значений.
Моделирование методом Монте-Карло требуется и тогда, когда не все распределения являются нормальными. Хотя другие типы распределений не входят в предмет данной книги, упомянем о двух из них - равномерном и бинарном (рис. 5, 6).
Рис. 5. Равномерное распределение (не идеальное, а построенное с помощью функции СЛЧИС в Excel)
Особенности:
- вероятность всех значений одинакова;
- распределение симметрично, без перекосов; медиана находится точно посредине между верхней и нижней границами интервала;
- значения за пределами интервала невозможны.
Для построения данного распределения в Excel была использована формула: СЛЧИС()*(UB – LB) + LB, где UB – верхняя граница; LB – нижняя граница; с последующим разбиением всех значений на диапазоны с помощью сводной таблицы.
Рис. 6. Бинарное распределение (распределение Бернулли)
Особенности:
- возможны только два значения;
- существует единственная вероятность одного значения (в данном случае 60%); вероятность другого значения равна единице минус вероятность первого значения
Для построения случайного распределения данного вида в Excel использовалась функция: =ЕСЛИ(СЛЧИС()<Р;1;0), где Р - вероятность выпадения «1»; вероятность выпадения «0» равна 1–Р; с последующим разбиением всех значений на два значения с помощью сводной таблицы.
Метод впервые использовал математик Станислав Улам (см. ).
Дуглас Хаббард далее перечисляет несколько программ, предназначенных для моделирования методом Монте-Карло. Среди них и Crystal Ball компании Decisioneering, Inc, Денвер, штат Колорадо. Книга на английском языке была издана в 2007 г. Сейчас же эта программа принадлежит уже Oracle . Демо-версия программы доступна для скачивания с сайта компании. О ее возможностях мы и погорим .
См. главу 5 упоминавшейся книги Дугласа Хаббарда
Здесь Дуглас Хаббард под размахом понимает разность между верхней границей 90%-ного доверительного интервала и средним значением этого интервала (или между средним значением и нижней границей, так как распределение симметрично). Обычно под размахом понимают разность между верхней и нижней границами.
Вернуться в Оглавление
ПРИМЕНЕНИЕ ТАБЛИЧНОГО ПРОЦЕССОРА MS EXCEL ДЛЯ ИЗУЧЕНИЯ МЕТОДА МОНТЕ-КАРЛО
Для моделирования различных физических, экономических и других процессов широко распространены методы, называемые методами Монте-Карло. В их основе лежит метод статистических испытаний. Суть его состоит в том, что результат испытания ставится в зависимость от значения некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания носит случайный характер.
Особенность метода состоит в том, что он гарантирует высокое качество статистических оценок только при весьма большом числе испытаний, которое невозможно выполнить без помощи компьютера.
Табличные процессоры не очень удобны для проведения расчетов Монте-Карло, однако с их использованием можно достаточно просто проиллюстрировать основные особенности этого метода.
Применение метода Монте-Карло для вычисления площади круга
Рассмотрим применение этого метода для вычисления площади круга заданного радиуса. Данная задача хорошо иллюстрирует возможности метода. Пусть круг имеет радиус R = 1 (рис. 1). Уравнение соответствующей окружности имеет вид: (x – 1)+ (y – 1)= 1. (1)
Для решения задачи методом Монте-Карло впишем круг в квадрат. Вершины квадрата будут иметь координаты (0,0), (2,0), (0,2), (2,2). Любая точка внутри квадрата или на его границе должна удовлетворять неравенствам 0 < x < 2 и 0 < y < 2 . При случайном заполнении квадрата точками, координаты которых распределены равномерно в этих интервалах, часть точек будет попадать внутрь круга. Если выборка состоит из n наблюдений и m точек попали внутрь круга или на окружность, то оценку площади круга S можно получить из
соотношения
S = S m / n (2)
где S – площадь квадрата, в который вписан круг.
В Excel с помощью функции СЛЧИС() можно получать равномерно распределенные случайные числа в диапазоне от 0 до 1. Для получения значений x и y в нужном диапазоне следует вводить формулы =2*СЛЧИС().
Число точек, попавших внутрь круга или на окружность, можно подсчитать, использовать функцию ЕСЛИ. Если координаты x и y таковы, что
(x – 1) + (y – 1) ≤ 1 , тогда функция будет возвращать 1, иначе 0. Тогда число m в формуле (2) для площади круга определится как сумма всех значений, возвращаемых функцией ЕСЛИ, а число n равно числу испытаний, которое можно подсчитать с помощью функции СЧЕТ. Только при большом числе испытаний можно получить близкое к точному значение равное π /4 =0, 7854.
Поэтому нужными формулами необходимо заполнить сразу большое число строк, например 500. Так будет выглядеть электронная таблица в режиме отображения формул:
| А | В | С | D | |
| Х | У | =СУММ(С3:С502) | =C1/C2 | |
| =СЧЁТ(С3:С502) | ||||
| =2*СЛЧИС() | =2*СЛЧИС() | =ЕСЛИ(А3^2+B3^2<=1;1;0) | ||
| … | … | … | … | |
| =2*СЛЧИС() | =2*СЛЧИС() | =ЕСЛИ(А502^2+В502^2<=1;1;0) |
В ячейке D1 будет находиться результат – площадь фигуры.
Вычисляя отношение m/n при нарастающем числе испытаний, можно сделать выводы, справедливые для любого статистического эксперимента независимо от природы и типа моделируемой системы:
С увеличением продолжительности наблюдения отклонение измеряемой
величины от ее точного значения уменьшается;
Существует предел, за которым увеличение продолжительности модели уже
не дает существенного повышения точности результата.
ЗАДАНИЕ
В соответствии с вариантом, методом Монте – Карло определить площадь фигур (см. рис. 1), и сравнить полученный результат с результатом, вычисленным по формуле.
| № варианта | |||||
| Фигура | Левая часть круга | Правая часть круга | Нижняя часть круга | Верхняя часть круга | Левая верхняя часть |
| № варианта | |||||
| Фигура | Левая верхняя часть круга | Правая верхняя часть круга | Правая нижняя часть круга | Левый верхний квадрант квадрата | Левый нижний квадрант квадрата |
| № варианта | |||||
| Фигура | Правый верхний квадрант квадрата | Правый нижний квадрант квадрата | Левый верхний треугольник | Правый верхний треугольник | Левый нижний треугольник |
| № варианта | |||||
| Фигура | Правый нижний треугольник | Верхняя половина квадрата | Нижняя половина квадрата | Левая половина квадрата | Правая половина квадрата |
Применительно к управлению Проектами, использование метода Монте – Карло позволяет нам оценить риск невыполнения проекта в срок или риск не уложиться в бюджет Проекта.
Рассмотрим сетевой график из лабораторной работы № и возьмем работы, формирующие критический путь.
| Работа | t о (i,j) | t нв (i,j) | t п (i, j): | t̄(i,j) |
| 0,1 | ||||
| 1,4 | ||||
| 4,5 | ||||
| 5,6 |
Длина критического пути равна 10 дням. Однако, учитывая, что каждая работа имеет оптимистическую и пессимистическую оценки длительности, встает вопрос, а какова вероятность выполнения Проекта за 10 дней или, например, за 12 дней?
Моделирование методом Монте-Карло – это способ решения подобных задач. Необходимо случайным образом выбрать в указанных интервалах (от t о (i,j) до t п (i, j)) длительностей работ значения, и рассчитать длительность Проекта. Одни результаты превысят 10 дней (или 12 дней), а другие окажутся меньше. Процент реализаций, не превышающих 10 дней (12 дней), и будет искомой вероятностью.
Для моделирования надо знать форму кривой распределения. Для разных величин больше подходят кривые одной формы, чем другой. Мы будем использовать кривую нормального (гауссова) распределения. Это колоколообразная кривая, на которой большинство возможных значений результатов группируются в центральной части графика и лишь немногие, менее вероятные, распределяются, сходя на нет к его краям (рис. 1).
Вот как выглядит нормальное распределение:

Рис.1. Нормальное распределение
Особенности:
Значения, располагающиеся в центральной части графика, более вероятны, чем значения по его краям;
Распределение симметрично; медиана находится точно посредине между верхней и нижней границами 90%-ного доверительного интервала (CI);
«хвосты» графика бесконечны; значения за пределами 90%-ного доверительного интервала маловероятны, но все же возможны.
Для построения нормального распределения в Excel можно воспользоваться функцией =НОРМРАСП(Х; Среднее; Стандартное_откл; Интегральная),
где Х – значение, для которого строится нормальное распределение;
Среднее – среднее арифметическое распределения; в нашем случае = 0;
Стандартное_откл – стандартное отклонение распределения; в нашем случае = 1;
Интегральная – логическое значение, определяющее форму функции; если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения; в нашем случае = ЛОЖЬ.
С нормальным распределением связано такое понятие, как стандартное отклонение. Рисунок 1 показывает, что в одном 90%-ном доверительном интервале насчитывается 3,29 стандартного отклонения.
В нашем примере создадим в электронной таблице генератор случайных чисел для каждого интервала значений (т.е. для каждой работы). Начнем с первой работы.
Воспользуемся формулой Excel: =НОРМОБР(вероятность;среднее;стандартное_откл),
где вероятность – вероятность, соответствующая нормальному распределению;
среднее – среднее арифметическое распределения;
стандартное_откл – стандартное отклонение распределения.
В нашем случае:
Среднее (медиана) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2 = (3+2)/2;
Стандартное отклонение = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29 = (3-2)/3,29.
Таким образом, формула имеет вид:
НОРМОБР(СЛЧИС();(3+2)/2;(3-2)/3,29),
где СЛЧИС – функция, генерирующая случайные числа в диапазоне от 0 до 1;
(3+2)/2 – среднее арифметическое диапазона MS;
(3-2)/3,29 – стандартное отклонение.
На рис. 2 представлен вариант исходных данных в Excel для данной задачи.

Рис. 2. Исходные данные для решения задачи
На рис. 3 представлена та же таблица в виде формул.

Рис.3. Таблица Excel с формулами
Предполагая, что количество экспериментов равно 100, заполним формулами 100 строчек – с 3 по 102.
Учитывая, что суммарная длина пути лежит в диапазоне от 7 до 14, а нам надо определить вероятность события, что мы выполним Проект за 10 (или 12) дней, разобьем весь диапазон на следующие отрезки: 7 и менее дней, от 7 до 10 дней, от 10 до 12 дней, от 12 до 14 дней, 14 и более дней. Формулы для подсчета попадания испытания в соответствующий интервал занесем в столбцы H,I,J,K,L.
Результаты представлены на рис. 4, а формулы для подсчета результатов и диаграмма, иллюстрирующая их, представлены на рис. 5.

Рис. 4. Результаты расчетов
 Рис. 5. Формулы для подсчета результатов и диаграмма
Рис. 5. Формулы для подсчета результатов и диаграмма
Итак, по результатам работы можно сделать вывод, что Проект с вероятностью 36% мы закончим за 10 дней и с вероятностью 89% (36%+53%) за 12 дней.
ЗАДАНИЕ
Рассчитать вероятность завершения Проекта (в соответствии с выбранным вариантом) за время t кр и за время, большее, чем t кр на 10%. (округлить в большую сторону до целого числа дней) . В качестве исходных данных, взять данные из лабораторной работы № .
СРСП 5 8
Тема:
■ Кто использует моделирование методом Монте-Карло?
■ Что произойдет, если я введу в какую-либо ячейку формулу =СЛЧИС() [- RANDQ ]?
■ Как мне смоделировать значения дискретной случайной величины?
■ Как мне смоделировать значения случайной величины с нормальным распределением?
■ На основе каких данных компания-производитель поздравительных открыток может определить, сколько открыток необходимо напечатать?
Нам хотелось бы точно оценивать вероятность точно неизвестных событий. Например, какова вероятность того, что у денежных потоков, связанных с новым товаром, будет положительная чистая приведенная стоимость (ЧПС) Каков риск вложений в наш инвестиционный портфель? Метод Монте-Карло позволяет нам моделировать ситуации, неопределенные в данный момент, и тысячи раз проиграть их на компьютере.
ПРИМЕЧАНИЕ Название «моделирование методом Монте-Карло» пришло к нам из в 1930-1940 гг., когда физики на компьютере моделировались ситуации для оценки вероятности того, что цепная реакция, необходимая для атомной бомбы, пройдет успешно. Специалисты, участвовавшие в этой работе, были страстными поклонниками азартных игр, они и дали операциям моделирования название «Монте-Карло».
В следующих пяти главах я на нескольких примерах покажу, как с помощью Excel реализовать моделирование методом Монте-Карло.
Основы моделирования методом Монте-Карло
Кто использует моделирование методом Монте-Карло?
Многие компании применяют моделирование методом Монте-Карло как важное средство принятия решений. Вот несколько примеров.
■ Компании General Motors , Procter and Gamble и Eli Lilly применяют моделирование для оценки как средней доходности, так и риска, связанного с выпуском новых товаров. В General Motors эта информация помогает главному исполнительному директору Рику Ваггонеру (Rick Waggoner ) определять товары, выпуском которых стоит заняться.
■ General Motors применяет моделирование для таких операций, как прогнозирование чистой прибыли корпорации, прогнозирование структурных затрат и затрат на приобретение, определение подверженности корпорации различным видам рисков (например, изменению процентных ставок и колебаниям валютного курса).
■ Lilly применяет моделирование для определения оптимальной производственной мощности, требуемой для производства каждого лекарства.
■ Компании с Wall Street применяют моделирование для оценки сложных финансовых показателей и суммы под риском (СПР) их инвестиционных портфелей.
■ Procter and Gamble применяет моделирование для примерной оценки и оптимального хеджирования (страхования) рисков, связанных с изменением курса иностранной валюты.
■ Sears применяет моделирование, чтобы оценить, сколько единиц каждого модельного ряда необходимо заказать у поставщиков - например, сколько пар Dockers следует заказать в этом году.
■ Моделирование можно использовать для оценки «реальных возможностей», например возможности развития, принятия обязательств или отсрочке проекта.
■ Специалисты по финансовому планированию применяют моделирование методом Монте-Карло, чтобы определять оптимальные инвестиционные стратегии для пенсионных вкладов.
Что произойдет, если я введу в какую-либо ячейку формулу =СЛЧИС()?
Если вы введете в какую-либо ячейку формулу =СЛЧИС(), то получите чи-. которое с одинаковой вероятностью может принять значение в диапазоне от 0 до 1. Таким образом, в примерно 25% случаев вы получите число, меньшее или равное 0,25; в 10% случаев - число не менее 0,90 и так далее. (рис. 1).
Рис. 1Демонстрация работы функции СЛЧИС (RAND )
Я скопировал из ячейки СЗ в С4:С402 формулу =СЛЧИС(). Диапазону СЗ:С402 я задал имя Данные. После этого в столбце F я вычислил среднее 400 случайных чисел (ячейка F 2) и с помощью функции СЧЁТЕСЛИ (COUNTIF определил долю чисел от 0 до 0,25, от 0,25 до 0,50, от 0,50 до 0,75 и от 0,75 до 1. Если вы нажмете клавишу F 9, случайные числа будут сгенерированы заново. Обратите внимание: среднее 400 случайных чисел всегда близко к 0,5 и примерно 25% результатов попадают в каждый интервал, равный 0,25. Эти результаты согласуются с определением случайных чисел. Заметьте также, что значения, генерируемые функцией СЛЧИС (RAND ) в разных ячейках, независим!: Например, если случайное число, сгенерированное в ячейке СЗ - большое (например, 0,99), это ничего не скажет нам о величине других сгенерированные случайных чисел.
Как мне смоделировать значения дискретной случайной величины?
Предположим, спрос на календари определяется следующей дискретной случайной величиной:
|
Спрос |
Вероятность |
|
10000 |
0,10 |
|
20000 |
0,35 |
|
40000 |
0,30 |
|
60000 |
0,25 |
Как нам заставить Excel многократно проиграть, или смоделировать, этот спрос на календари? Хитрость в том, чтобы связать каждое возможное значе ние функции СЛЧИС ( RAND ) с возможным спросом на календари. Следую щее с опоставление гарантирует, что спрос на 10000 штук реализуется в 10% случаев и так далее.
спрос Присвоенное случайное число
|
10000 |
Меньше 0,10 |
|
20000 |
Больше или равно 0,10 и меньше 0,45 |
|
40000 |
Больше или равно 0,45 и меньше 0,75 |
|
60000 |
Больше или равно 0,75 |
Чтобы посмотреть, как моделируется спрос, откройте рис. 2.

Рис. 2 Пример моделирования дискретной случайной величины
Основной принцип нашего моделирования - воспользоваться случайным числом для просмотра в диапазоне таблицы F 2: G 5 (ему дано имя поиск). Случайные числа, большие или равные 0 и меньшие 0,10, соответствуют спросу в 10000 штук; случайные числа, большие или равные 0,10 и меньшие 0,45 соответствуют спросу в 20000 штук; случайные числа, большие или равные XI0, и меньшие 0,75, соответствуют спросу в 40000 штук; случайные числа, большие или равные 0,75, соответствуют спросу в 60000 штук. Я сгенерировал 400 случайных чисел, скопировав из ячейки СЗ в С4:С402 формулу СЛЧИС() [ RAND ()]. Затем я сгенерировал 400 испытаний, или итераций, скопировав из ячейки ВЗ в В4:В402 формулу ВПР(СЗ;поиск;2). Эта формула гарантирует, что любое случайное число меньше 0,10 сгенерирует спрос, равный 10000 ; любое случайное число в диапазоне от 0,10 до 0,45 сгенерирует спрос, равный 20000 единицам и так далее. В диапазоне ячеек F 8: F 11 я с помощью функции СЧЁТЕСЛИ (COUNTIF ) определил долю каждого значения спроса в аших 400 итерациях. Обратите внимание: когда бы вы ни нажали клавишу F 9 для повторной генерации случайных чисел, моделируемые вероятности оказываются близки к нашим предполагаемым вероятностям спроса.
Как мне смоделировать значения случайной величины с нормальным распределением?
Введя в какую-либо ячейку формулу НОРМОБР(СЛЧИС();мю;сигма), вы делируете значение случайной величины с нормальным распределением, нее значение которой равно мю и стандартное отклонение - сигма. (рис. 3).

Рис. 3 Моделирование случайной величины с нормальным распределением
Предположим, нам требуется смоделировать 400 испытаний, или итераций, для случайной величины с нормальным распределением, среднее которой равно 40000, а стандартное отклонение - 10000 (я ввел эти значения в ячейки Е1 и Е2, и задал им имена среднее и станд. откл. соответственно l Скопировав формулу =СЛЧИС() из ячейки С4 в С5:С403, я сгенерировал 400 разных случайных чисел. Скопировав из ячейки В4 в В5:В403 формулу НОРМОБР (С4 ;среднее;сигма), я сгенерировал 400 итераций для случайной ве личины с нормальным распределением, среднее которой равно 40000, а стандартное отклонение - 10000. Когда мы нажимаем клавишу F 9 для повторной генерации случайных чисел, среднее остается близким к 40000, а стандартнее отклонение - близким к 10000.
По сути, для случайного числа х формула НОРМОБР(р;мю;сигма) генерирует р-ю персентиль случайной величины с нормальным распределение^ среднее которой равно мю, а стандартное отклонение - сигма. Например, сп -чайное число 0,73 в ячейке В13 (рис. 58-3) генерирует примерно 73-ю персентиль случайной величины с нормальным распределением, среднее которой равно 40000, а стандартное отклонение равно 10000.
На основе каких данных компания-производитель поздравительных открыток может определить, сколько открыток необходимо напечатать?
Метод Монте-Карло по могает принимать лучшие бизнес-решения. Предположим, спрос на открытки ко Дню Св. Валентина определяется следующей дискретной случайной в личиной:
Основы моделирования методом Монте-Карло
|
Спрос |
Вероятность |
|
10000 |
0,10 |
|
10000 |
0,35 |
|
40000 |
0,30 |
|
6 0000 |
0,25 |
Поздравительная открытка продается по цене $4,00, а переменные издержки на производство одной открытки составляют $1,50. Нереализованные открытки должны быть распроданы по цене $0,20 за штуку. Сколько открыток следует напечатать?
В сущности, мы моделируем каждый возможный объем производства (10000, 20000, 40000 и 60000 штук) множество раз (скажем, 1000 итераций). Затем мы определяем, какой объем обеспечивает максимальный средний доход для этих 1000 итераций. (рис. 4). Я назначил ячейкам С1:С11 имена диапазонов из ячеек 31:В11. Диапазону G 3: H 6 я назначил имя поиск. Наши параметры цены реализации и затрат указаны в ячейках С4:С6.

Рис. 4 Моделирование объема производства открыток ко Дню Св. Валентина
Пробный объем производства (в данном примере - 40000) в ячейку С1. Затем я сгенерировал случайное число в ячейке С2 с помощью форму-:ы =СЛЧИС(). Как я уже говорил, я моделирую спрос на открытку в ячейке 1: по формуле ВПР(случайное_число;понск;2) [в формуле ВПР ( VLOOKUP ) случайное_число - это имя, назначенное ячейке С2, а не функция СЛЧИС RAND )].
Число проданных открыток меньше нашего объема производства и спроса . В ячейке С8 я подсчитываю наш доход по формуле МИН (объем_производства;спрос) *цена_открытки. В ячейке С9 я вычисляю общие затраты на производство по формуле объем_производства*себестоимостъ_пр_ва_открытки.
Если мы производим открыток больше, чем нужно, число нереализованных открыток равно объему производства минус спрос; в противном случае -нереализованных открыток не будет. Мы вычисляем затраты на переработку в ячейке С10 по формуле =стоимостъ_при_распродаже*ЕСЛИ(объем_производ-опва>спрос;объем_производства-спрос;0). И, наконец, в ячейке СП мы вычисляем нашу прибыль по формуле =доход-общие_переменные_издержки-с щие_издержки_на_распродажу.
Нам требуется эффективный способ имитации многократного (скажи 1000 раз) нажатия клавиши F 9 и подсчета дохода для каждого объема производства. В этом случае нас спасет таблица подстановки с двумя переменными. Таблица подстановки, ис пользованная мной в данном примере, показана на рис. 5.

Рис. 5 Таблица подстановки с двумя переменными для моделирования объема производства поздравительных открыток
В диапазоне ячеек А16:А1015 я ввел числа от 1 до 1000 (соответствующие 1000 испытаний). Один из простых способов создать эти значения - ввести 1 в ячейку А16 и затем выбрать в меню Правка ( Edit ) команду Заполнить\Прог-рессия (Fill \ Series ). В поле Шаг ( Step value ) диалогового окна Прогрессия ( Series ) (рис. 58-6) введите 1, а в поле Предельное значение (Stop value ) - 1000. Установите переключатель по столбцам ( Columns ) и затем щелкните Столбец А, начиная с ячейки А16, будет заполнен числами от 1 до 1000.
Затем следует ввести возможные объемы производства (10000, 20000. 40000 и 60000 единиц) в ячейки В15:Е15. Мы хотим вычислить прибыль для каждого испытания (от 1 до 1000) и каждого объема производства. В верхней левой ячейке (А15) нашей таблицы подстановки мы ссылаемся на форм прибыли, которая задана в ячейке С11, вводя =С11.
Теперь все готово и мы можем заставить Excel моделировать 1000 итераций спроса для каждого объема производства. Выделите диапазон таблицы (А15:Е1014) и затем щелкните в меню Данные ( Data ) команду Таблица подстановки (Table ). Чтобы создать таблицу подстановки с двумя параметрами мы указываем в качестве ячейки для подстановки по строкам любую пустую ячейку (в данном случае - 114), а в качестве ячейки для подстановки по столбцам - объем производства (О). После того как вы щелкнете OK , Excel смоделирует 1000 значений спроса для каждого объема производства.


Рис. 6 С помощью диалогового окна Прогрессия ( Series )и вставьте номера испытаний от 1 до 10ОО
Чтобы понять, почему это работает, рассмотрим значения, полученные в таблице подстановки (диапазон ячеек С16:С1015). Для каждой из этих ячеек Excel подставляет значение 20000 в ячейку С1. В С16 в пустую ячейку помещается значение, подставляемое по строкам (1), и случайное число в ячейке С2 генерируется заново. После этого в ячейку С16 записывается соответствующее значение прибыли. Затем в пустую ячейку снова помещается значение, подставляемое по строкам (2), и случайное число в ячейке С2 генерируется заново. Соответствующее значение прибыли записывается в ячейку С17.
Скопировав из ячейки В13 в С13:Е13 формулу СРЗНАЧ(В16:В1015), мы подсчитаем среднюю прибыль для каждого объема производства. Скопировав формулу СТАНДОТКЛОН(В16:В1015) из ячейки В14 в диапазон С14:Е14, мы вычисляем стандартное отклонение прибыли для каждого объема производства. При каждом нажатии клавиши F 9 для всех объемов производства моделируются 1000 итераций спроса. Производство 40000 открыток всегда обеспечивает максимальную прибыль. Следовательно, ясно, что производство 40000 - правильное решение.
Влияние риска на наше решение. Если мы напечатаем 20000 открыток вместо 40000, наша ожидаемая прибыль упадет примерно на 22%, однако наш риск измеряемый стандартным отклонением прибыли) упадет практически на 3%. Следовательно, если риск для нас крайне неприемлем, печать 20000 открыток может оказаться правильным решением. Кстати, при печати 10000 открыток стандартное отклонение всегда равно нулю, поскольку мы в любом случае продадим их, и ничего не останется.
ПРИМЕЧАНИЕ На этом листе я установил переключатель Вычисления ( Excelulation ) в положение автоматически кроме таблиц ( Automatic Except For Tables ) [см. вкладку Вычисления ( Excelulation ) диалогового окна Параметры ( Options )]. В результате таблица подстановки не будет пересчитывать значения, пока мы не нажмем клавишу F 9. Отличная идея, поскольку при большом объеме таблицы подстановки ваша работа замедлится, если Excel будет каждый раз пересчитывать значения при вводе новых данных в ячейки листа. Обратите внимание: в этом примере при каждом нажатии клавиши F 9 средняя прибыль изменяется. Это происходит потому, что каждом нажатии клавиши F 9 значения спроса для всех казанных объемов производства генерируются на основе новой последовательности из 1000 случайных чисел.
Доверительный интервал для средней прибыли. Естественный вопрос, возникающий в данной ситуации: «Для какого интервала значений мы можем быть уверены на 95%, что средняя прибыль верна?» Этот интервал называется 95-процентным доверительным интервалом для средней прибыли. Для среднего значения вывода любой операции моделирования 95-процентный доверительный интервал вычисляется по формуле:
Средняя прибыль±
1,96*стандартное отклонение прибыли ■у ]число итераций
В ячейке J 11 я вычислил нижнюю границу 95-процентного доверительного интервала для средней прибыли при производстве 40000 открыток, воспользовавшись формулой D 13- l ,96* D 14/ KOPEHb (1000). В ячейке J 12 я вычислил верхнюю границу 95-процентного доверительного интервала по формуле D 13+ l ,96* D 14/ KOPEHb (1000). Эти вычисления показаны на рис. 7.

Рис. 7 Девяностопятипроцентный доверительный интервал для средней прибыли при производстве 40000 открыток
Мы на 95% уверены, что средняя прибыль при производстве 40000 календарей составит от $56578 до $62445.
Самостоятельно
1. Дилер General Motors Company считает, что спрос на модель « Envoy » выпуска 2005 г. будет распределен по нормальному закону со средним, равным 200, и стандартным отклонением, равным 30. Его затраты на выпуск одной машины модели Envoy составляют $25000, и продает он ее по $40000. Половину всех нереализованных машин модели Envoy можно продать по $30000. В качестве возможного размера заказа дилер рассматривает 200, 220, 240, 260, 280 и 300 машин модели Envoy . Сколько машин ей следует заказать?
Небольшой супермаркет пытается определить, сколько копий журнала «Реор1е» им следует заказывать каждую неделю. Они считают, что спрос на «Реор1е» в магазине регулируется следующей дискретной случайной величиной:
|
Спрос |
Вероятность |
|
0,10 |
|
|
0,20 |
|
|
0,30 |
|
|
0,25 |
|
|
0,15 |
Супермаркет покупает каждую копию «Реорк» за $1,00 и продает ее по $1,95. Каждую нереализованную копию «Реор1е» они могут вернуть за $0,50. Сколько копий журнала «Реор1е» следует заказать супермаркету?
Цели:
образовательные: изучение численного метода Монте–Карло.
развивающие:
- научить анализировать при нахождении общего, частного в понятиях информатики и ЭТ;
- научить рассуждать;
- составлять алгоритм задач;
- уметь составлять формулы.
воспитательные: воспитание познавательного интереса к предмету путем введения новейших технологий обучения
Ход урока
I. Оргмомент.
Цель нашего урока – это знакомство с функцией случайного числа и применением метода Монте–Карло в электронных таблицах.
II. Усвоение новых знаний.
В математике для решения задач часто требуются математические модели. Одна из таких задач – вычисление площадей. Конечно для простейших фигур (прямоугольников, многоугольников, кругов) вычисление площади не составляет труда: надо в известные формулы подставить исходные данные. А как быть если фигура имеет сложные формы? Итак, задача: Дана фигура сложной формы. Вычислить её площадь.
Можно предложить разные модели для этой задачи. Например, в 6-м классе вас учили использовать палетку: на фигуру накладывается клетчатая прозрачная бумага или плёнка (палетка), и подсчитывается количество квадратиков, попавших в фигуру. В этой модели предполагается, что чем меньше клетки, тем точнее будет результат, независимо от того, каким образом наложить палетку на фигуру.
Можно придумать “физическую” модель, скопировать фигуру на картон, аккуратно вырезать её, взвесить и поделить на вес единичного квадрата из этого же картона.
В 11-м классе вы познакомитесь ещё с одним способом нахождения площадей фигур: с помощью интегралов.
Однако все эти модели трудно поддаются расчётам на ЭВМ. Мы попробуем построить математическую модель, которая позволит эффективно применять ЭВМ для решения задач на нахождение площадей, объемов и тому подобное.
Поместим данную фигуру в квадрат. Будем наугад (как говорят математики, случайным образом) бросать точки в этот квадрат. Естественно, что чем больше площадь фигуры, тем чаще в неё будут попадать точки. Представьте себе квадратный дворик и в нем детскую круглую площадку. Каждому ясно, что во время снегопада количество снежинок, попавших на детскую площадку, пропорционально её площади. Таким образом, можно сделать допущение: при большом числе точек, наугад выбранных внутри квадрата, доля точек, содержащихся в данной фигуре, приближенно равна отношению площади квадрата.
Такой метод приближенного нахождения площадей фигур носит название метода Монте–Карло (по названию города, где расположена знаменитая рулетка, которую можно рассматривать как “генератор” случайных чисел).
Только случайность поможет нам найти площадь фигуры методом Монте–Карло.
В Exсel имеется возможность проводить моделирование с использованием случайных чисел.
Функция СЛЧИС() (без аргументов) генерирует случайное число в диапазоне от 0 до 1. Совокупность этих чисел равномерно распределена на отрезке . При нажатии функциональной клавиши F9 (пересчет) в ячейках, содержащих формулу с функцией СЛЧИС , генерируется новое случайное число.
Показываю на ЭВМ (увеличив размер шрифта).
Вводим в ячейку формулу =СЛЧИС() и нажимаю F9 . В ячейках изменяется выводимое число.
Вопрос: Как изменить формулу, чтобы диапазон расширился от 0 до 10?
Ответ: Нужно умножить на 10, то есть =СЛЧИС()*10 .
Вопрос: Как изменить формулу, чтобы диапазон расширился от 2 до 3?
Ответ: Нужно сложить с числом 2, то есть =СЛЧИС()+2 .
Вопрос: Как изменить формулу, чтобы диапазон лежал на промежутке ?
Ответ: =(10–5)*СЛЧИС()+5 .
Вопрос: Как изменить формулу, чтобы диапазон лежал на промежутке ?
Ответ: Нужно записать формулу следующего вида =(b–a)*СЛЧИС()+a .
III. Проверка понимания материала. (Раздаю тесты.)
Тест на функцию генератор случайных чисел.
Вариант 1
Вопрос 1.
- =СРЗНАЧ(A1: A5) .
- =СЧЕТ(А1: А4) .
- =ЕСЛИ(В1>В2; 1; 0) .
- =(В – А)*СЛЧИС()+А .
Вопрос 2. Дана формула = СЛЧИС()* 1.4+3.2 .
- [ 0; 3,2 ].
- [ 1,4; 3,2 ].
- [ 3,2; 4,6 ].
- [ 0; 4,6 ].
Вопрос 3. Дана формула = СЛЧИС()* 50 .
В каком диапазоне будут получены числа.
- [ 0; 1 ].
- [ 0; 50 ].
- [ 1; 50 ].
- (0; 50).
Вопрос 4. Дана формула = (100 – 20)* СЛЧИС()+20 .
В каком диапазоне будут получены числа.
- [ 0; 20 ].
- [ 0; 100 ].
- [ 20; 100 ].
- [ 80; 100 ].
Вопрос 5.
Вопрос 6. Дана формула = СЛЧИС()+12 .
В каком диапазоне будут получены числа.
- [ 0; 12 ].
- [ 1; 12 ].
- [ 11; 13 ].
- [ 12; 13 ].
Вариант 2
Вопрос 1. Дана формула = СЛЧИС()* 30 .
В каком диапазоне будут получены числа.
- [ 0; 1 ].
- [ 0; 30 ].
- [ 1; 30 ].
- (0; 30) .
Вопрос 2. Дана формула = СЛЧИС()* 3.2+1.4 .
В каком диапазоне будут получены числа.
- [ 0; 1,4 ].
- [ 1,4; 3,2 ].
- [ 3,2; 4,6 ].
- [ 1,4; 4,6 ].
Вопрос 3. Выберите из предложенных выражений формулу, определяющую числа случайным образом:
- =СРЗНАЧ(B1: B5) .
- =ЕСЛИ(В1>В2; 1; 0) .
- =СЛЧИС()+А .
- =СЧЕТ(А1: А4) .
Вопрос 4. Дана формула = (50 – 10)* СЛЧИС()+10 .
В каком диапазоне будут получены числа.
- [ 0; 10 ].
- [ 0; 50 ].
- [ 10; 40 ].
- [ 10; 50 ].
Вопрос 5. Дана формула = 21+ СЛЧИС() .
В каком диапазоне будут получены числа.
- [ 0; 21 ].
- [ 1; 21 ].
- [ 21; 22 ].
- [ 21; 23 ].
Вопрос 6. Какую функциональную клавишу необходимо использовать для изменения выводимых случайных чисел.
Ответы.
Вариант 1 . 1.4, 2.3, 3.2, 4.3, 5.4, 6.4.
Вариант 2. 1.2, 2.4, 3.3, 4.4, 5.3, 6.3.
IV. Подготовка к практической работе.
Давайте вычислим число p методом Монте–Карло. Для этого вспомним формулу площади круга. Назовите её. Ответ: S = R 2 Посмотрите на рис. 1.

Пусть окружность вписана в квадрат со стороной а = 2. Скажите, пожалуйста, чему равен радиус окружности? (Ответ: 1). Тогда площадь круга чему будет равна? (Ответ: S = ).
Рассмотрим единичный квадрат, вершины которого имеют координаты (0,0), (1,0), (1,1), (0,1). В квадрат будем бросать точку со случайными координатами. Этот квадрат высекает из окружности единичного радиуса с центром в начале координат сектор, площадь которого составляет четверть площади окружности, то есть /4.
Вспомним уравнение окружности с центром в начале координат.
Вопрос: Назовите запись данного факта. Ответ: x 2 + y 2 = 1.
Если точка оказалась внутри сектора, то фиксируем “удачное попадание” единицей, если точка оказалась вне сектора, записываем нуль.
Значит, если x 2 + y 2 < = 1, то точка попадает в круг, иначе она вне круга. Это и есть математическое соотношение, позволяющее определить, лежит ли точка в фигуре. После многократных бросаний вычислим отношение числа удачных исходов к общему количеству бросаний. Это число умножим на 4. Получим приближение к числу p .
Компьютерная модель .
Организуем вычисления на рабочем листе.
В ячейки А1 и В1 поместим заголовки x и y. В ячейку А2 поместим формулу генератора случайного числа =СЛЧИС() и скопируем ее до ячейки В1001 .
В ячейку С2 введем формулу, которая описывает условие попадания или не попадания точек в сектор, то есть =Если(А2^2+B2^2 < = 1; 1; 0) cкопируем до С1001 .
В ячейку С1002 разместим формулу подсчета удачных исходов =СУММ(С2:С1001)/250 или a / 250 . Таблица сконструирована. Теперь проведем компьютерный эксперимент.
Теперь нажимая F9 в ячейке С1002 сменяют друг друга десятичные приближения (не слишком точные) числа .
| A | B | C | |
| 1 | x | y | попадание |
| 2 | =СЛЧИС() | =СЛЧИС() | =ЕСЛИ(A2^2+B2^2 <= 1; 1; 0) |
| 3 | =СЛЧИС() | =СЛЧИС() | =ЕСЛИ(A3^2+B3^2 <= 1; 1; 0) |
| … | … | … | |
| 1001 | =СЛЧИС() | =СЛЧИС() | =ЕСЛИ(A1001^2+B1001^2 <= 1; 1; 0) |
| 1002 | =СУММ(С2:С1001)/250 |
V. Подведение итога.
Сегодня мы познакомились с методом Монте–Карло, провели компьютерный эксперимент и нашли практически значение числа ПИ.




